TFHE Deep Dive - Part IV - Programmable Bootstrapping

> Part I: Ciphertext types
> Part II: Encodings and linear leveled operations
> Part III: Key switching and leveled multiplications
> Part IV: Programmable Bootstrapping

This blog post is part of a series of posts dedicated to the Fully Homomorphic Encryption scheme called TFHE (also known as CGGI, from the names of the authors Chillotti-Gama-Georgieva-Izabachène). Each post will allow you to go deeper into the understanding of the scheme. The subject is challenging, we know! But don’t worry, we will dive into it little by little!

Disclaimer: If you have watched the video TFHE Deep Dive, you might find some minor differences in this series of blog posts. That’s because here there is more content and a larger focus on examples. All the dots will connect in the end!

We finally arrived to the last blog post of the series, the one dedicated to bootstrapping. In the first blog post we introduced all the ciphertext types used in TFHE, in the second one we saw how to perform homomorphic additions, multiplications by small constants and how to encode information, and in the third one we described key switching, homomorphic multiplications and we finally spoke about the CMux operation.

Now that we have all these ingredients, we are finally ready to build the most complex operation. We need three more additional building blocks -- the modulus switching, the sample extraction and the blind rotation -- and then we will be good to go.

Modulus Switching

The modulus switching is a very simple operation, largely used in the majority of FHE schemes. It consists, as the name of the operation suggests, in switching the ciphertext modulus to a new one. It is an operation that, in TFHE, is mainly used on LWE ciphertexts, but it could be extended to GLWE ciphertexts if necessary.

As in the previous blogposts, let $p$ and $q$ be two positive integers (powers of $2$ for simplicity), such that $p\leq q$ and let $\Delta = q/p$. Let’s recall that an LWE ciphertext encrypting a message $m \in \mathbb{Z}_p$ under the secret key $\vec{s} = (s_0, \ldots, s_{n-1}) \in \mathbb{Z}^n$ is a tuple:
$$
c = (a_0, \ldots, a_{n-1}, b) \in LWE_{\vec{s}, \sigma}(\Delta m) \subseteq \mathbb{Z}_q^{n+1}
$$
where the elements $a_i$ for $i\in [0..n-1]$ are sampled uniformly random from $\mathbb{Z}_q$, and $b = \sum_{i=0}^{n-1} a_i \cdot s_i + \Delta m + e \in \mathbb{Z}_q$, and $e \in \mathbb{Z}_q$ has coefficients sampled from a discrete Gaussian distribution $\chi_{\sigma}$. For simplicity, let's note $b = a_{n}$.

Then, let's consider another positive integer $\omega$: the modulus switching from $q$ to $\omega$ is the operation that takes all the components of the LWE ciphertext and switches their modulus from $q$ to $\omega$ as follows:
$$
\tilde{a}_i = \left\lfloor \frac{\omega \cdot a_i}{q} \right\rceil \in \mathbb{Z}_\omega.
$$
The result of this operation is a new LWE ciphertext:
$$
\tilde{c} = (\tilde{a}_0, \ldots, \tilde{a}_{n-1}, \tilde{a}_n = \tilde{b}) \in LWE_{\vec{s}, \sigma}(\tilde{\Delta} m) \subseteq \mathbb{Z}_\omega^{n+1}.
$$
In TFHE we generally switch to a smaller modulus $\omega$ equal to a power of $2$ and such that $p < \omega < q$, so $\tilde{\Delta} = \frac{\omega \cdot \Delta}{q} = \omega/p$. If $\omega$ is not a power of $2$, some rounding is applied.

The effect of this operation is to keep the $\log_2(\omega)$ MSB of the original ciphertext: the message is in fact encoded in the MSB in TFHE. However, by doing so, the noise grows quite a lot (it actually gets closer to the message) so it should be used very carefully if we do not want to compromise the message.

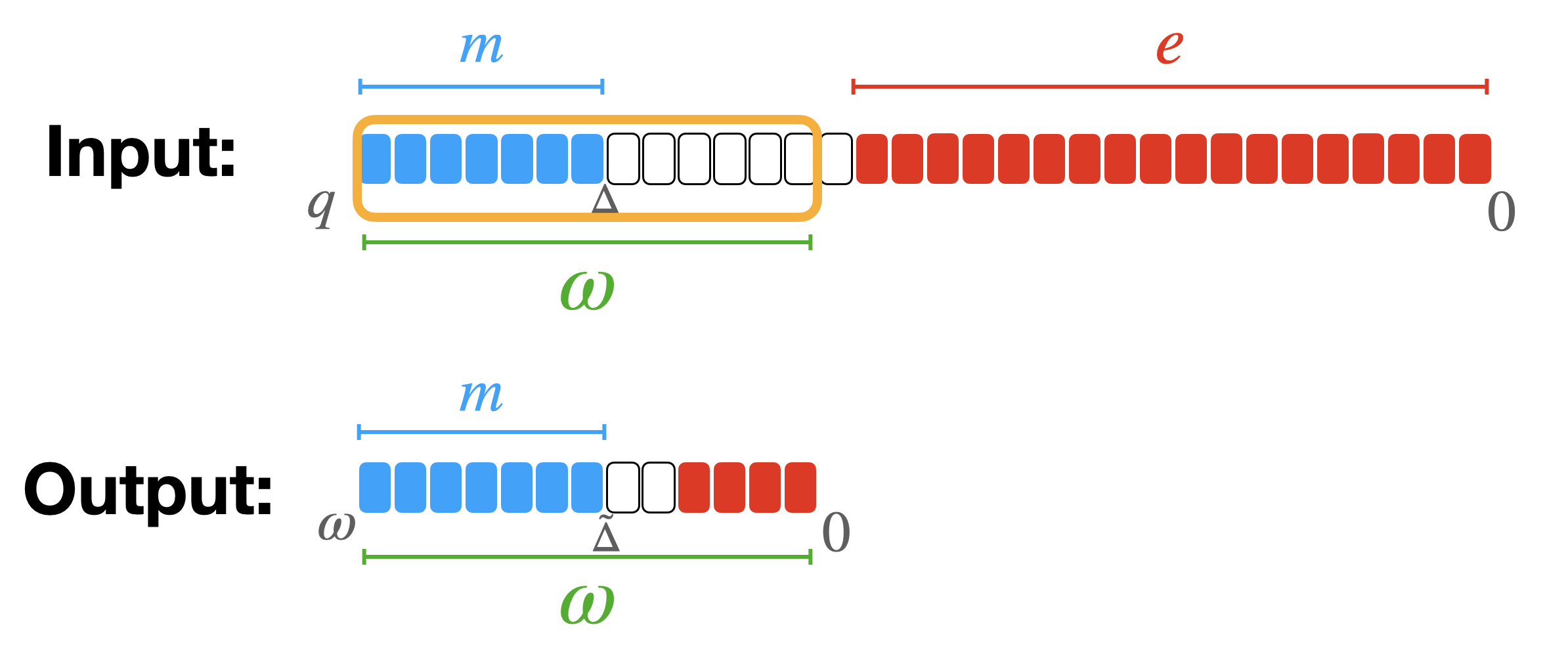
Toy Example

Let's make a small toy example to fix the ideas. For this toy example, let’s choose $q=64$, $p=4$ so $\Delta = q/p = 16$. Let also chose $n = 4$. We sample the secret key with uniform binary distribution as $n$ integers:
$$
\vec{s} = (s_0, s_1, s_2, s_3) = (0, 1, 1, 0) \in \mathbb{Z}^4.
$$
Let’s encrypt a message $m = 1 \in \mathbb{Z}_p$ by sampling $4$ uniformly random integer masks with coefficients in $\{ -32, -31, \ldots,$ $ -1, 0, 1, 2, \ldots, 30, 31 \}$:
$$
(a_0, a_1, a_2, a_3) = (-25, 12, -3, 7) \in \mathbb{Z}_q^n
$$
and discrete Gaussian Errors (small coefficients):
$$
E = 1 \in \mathbb{Z}_q.
$$

Then, we need to compute the body as:
$$
b = a_0 s_0 + a_1 s_1 + a_2 s_2 + a_3 s_3 + \Delta m + e = 26 \in \mathcal{R}_q
$$
So the encryption is:
$$
c = (a_0, a_1, a_2, a_3, b) = (-25, 12, -3, 7, 26) \in \mathbb{Z}^{n+1}_q.
$$

Now, let's perform the modulus switching by choosing $\omega = 32$:
$$
\tilde{c} = (\tilde{a}_0, \tilde{a}_1, \tilde{a}_2, \tilde{a}_3, \tilde{b}) = (-13, 6, -2, 4, 13) \in \mathbb{Z}^{n+1}_\omega.
$$
The new scaling factor is $\tilde{\Delta} = 8$. So let's try to decrypt this new ciphertext. As usual we start by computing:
$$
\tilde{b} - \sum_{i=0}^{n-1} \tilde{a}_i \cdot s_i = 9 \in \mathbb{Z}_q
$$
and then we rescale and round with the new $\tilde{\Delta}$:
$$
\lfloor 9/8 \rceil = 1 \in \mathbb{Z}_p
$$
which is the message we originally encrypted. Observe that the new error is equal to $1$ ($\tilde{\Delta} m + \tilde{e} = 8 \cdot 1 + 1$). It is not bigger than the original error that was equal to 1 as well, in absolute value, but we say that it has increased because its distance to the message has been reduced by the modulus switching (the scaling factor has changed).

Sample Extraction

The second building block we construct is another very simple operation called sample extraction. A sample extraction is an operation that takes as input a GLWE ciphertext, encrypting a polynomial message, and extracts the encryption of one of the coefficients of the message as a LWE ciphertext.

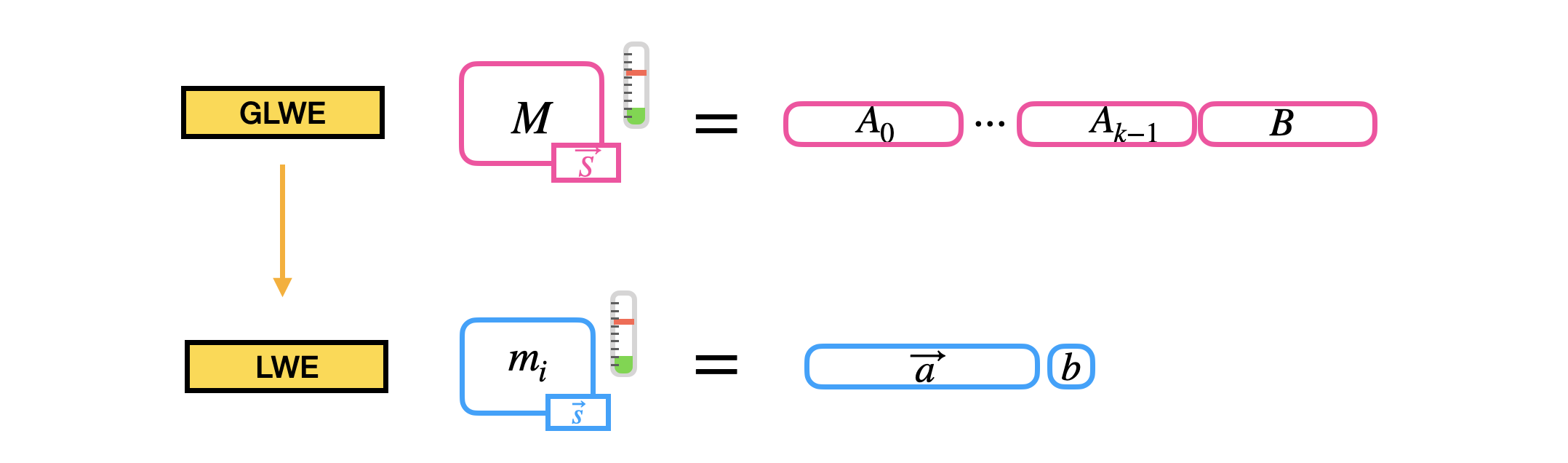
The operation does not increase the noise and simply consists in "copy-pasting" some of the coefficients of the GLWE ciphertext into the output LWE ciphertext. Let's check in detail!

Let’s take a GLWE ciphertext encrypting a message $M = \sum_{j=0}^{N-1} m_j X^j \in \mathcal{R}_p$ under the secret key $\vec{S} = (S_0 = \sum_{j=0}^{N-1} s_{0,j} X^j, \ldots, S_{k-1} = \sum_{j=0}^{N-1} s_{k-1,j} X^j) \in \mathcal{R}^k$, which is a tuple:
$$
C = \left(A_0 = \sum_{j=0}^{N-1} a_{0,j} X^j, \ldots, A_{k-1} = \sum_{j=0}^{N-1} a_{k-1,j} X^j, B = \sum_{j=0}^{N-1} b_j X^j \right) \in GLWE_{\vec{S}, \sigma}(\Delta M) \subseteq \mathcal{R}_q^{k+1}
$$
where the elements $A_i$ for $i\in [0..k-1]$ are sampled uniformly random from $\mathcal{R}_q$, and $B = \sum_{i=0}^{k-1} A_i \cdot S_i + \Delta M + E \in \mathcal{R}_q$, and $E \in \mathcal{R}_q$ has coefficients sampled from a Gaussian distribution $\chi_{\sigma}$.

Imagine that we want to extract the $h$-th coefficient of the message $M$, with $0 \leq h < N$. The result LWE ciphertext will have $n = k N$ and will be encrypted under the extracted secret key $\vec{s}$, equal to a copy-paste of the coefficients of the GLWE secret key:
$$
\vec{s} = (s_{0,0}, \ldots, s_{0,N-1}, \ldots, s_{k-1,0}, \ldots, s_{k-1,N-1}) \in \mathbb{Z}^{kN}.
$$
Then, we build the result LWE ciphertext $c = (a_0, \ldots, a_{n-1}, b) \in \mathbb{Z}^{n+1}_q$ by simply copying (some of) the coefficients  of the GLWE as follows:
$$
\begin{cases}
a_{N\cdot i + j} \leftarrow a_{i,h-j} &\text{ for } 0 \leq i < k, 0 \leq j \leq h \\
a_{N\cdot i + j} \leftarrow - a_{i,h-j+N} &\text{ for } 0 \leq i < k, h+1 \leq j < N \\
b \leftarrow b_h & \\
\end{cases}
$$

Toy Example

Why this operation works? In this toy example we will try to show why this is correct and give you the intuition so you don't have to always remember the complicated copy-paste rule.  

Let's use a generic RLWE ciphertext (so $k = 1$) as a toy example, and let's choose $N = 4$ for simplicity. A RLWE ciphertext encrypting a message $M = \sum_{j=0}^{3} m_j X^j \in \mathcal{R}_p$ under the secret key $S = \sum_{j=0}^{3} s_{j} X^j \in \mathcal{R}^k$ is a tuple:
$$
C = \left(A = \sum_{j=0}^{3} a_{j} X^j, B = \sum_{j=0}^{3} b_j X^j \right) \in RLWE_{\vec{S}, \sigma}(\Delta M) \subseteq \mathcal{R}_q^{2}
$$
where $B = A \cdot S + \Delta M + E \in \mathcal{R}_q$.

To understand sample extraction, let's try to observe in detail what happens during the first step of the decryption of this ciphertext. Recall that computations are done modulo $X^4 + 1$, so $X^4 \equiv -1$:
$$
\begin{aligned}
B - A \cdot S
&= (b_0 + b_1 X + b_2 X^2 + b_3 X^3) - (a_0 + a_1 X + a_2 X^2 + a_3 X^3) \cdot ({\color{red} s_0} + {\color{green} s_1} X + {\color{orange} s_2} X^2 + {\color{cyan} s_3} X^3) \\
&= (b_0 - a_0 {\color{red} s_0} + a_1 {\color{cyan} s_3} + a_2 {\color{orange} s_2} + a_3 {\color{green} s_1}) \\
&\hspace{0.3cm} + (b_1 - a_0 {\color{green} s_1} - a_1 {\color{red} s_0} + a_2 {\color{cyan} s_3} + a_3 {\color{orange} s_2}) \cdot X \\
&\hspace{0.3cm} + (b_2 - a_0 {\color{orange} s_2} - a_1 {\color{green} s_1} - a_2 {\color{red} s_0} + a_3 {\color{cyan} s_3}) \cdot X^2 \\
&\hspace{0.3cm} + (b_3 - a_0 {\color{cyan} s_3} - a_1 {\color{orange} s_2} - a_2 {\color{green} s_1} - a_3 {\color{red} s_0}) \cdot X^3 \\
&= (b_0 - a_0 {\color{red} s_0} + a_3 {\color{green} s_1} + a_2 {\color{orange} s_2} + a_1 {\color{cyan} s_3}) \hspace{2cm} \text{// just reorder the elements in the sum} \\
&\hspace{0.3cm} + (b_1 - a_1 {\color{red} s_0} - a_0 {\color{green} s_1} + a_3 {\color{orange} s_2} + a_2 {\color{cyan} s_3}) \cdot X \hspace{1.1cm} \text{// just reorder the elements in the sum} \\
&\hspace{0.3cm} + (b_2 - a_2 {\color{red} s_0} - a_1 {\color{green} s_1} - a_0 {\color{orange} s_2} + a_3 {\color{cyan} s_3}) \cdot X^2 \hspace{1cm} \text{// just reorder the elements in the sum} \\
&\hspace{0.3cm} + (b_3 - a_3 {\color{red} s_0} - a_2 {\color{green} s_1} - a_1 {\color{orange} s_2} - a_0 {\color{cyan} s_3}) \cdot X^3 \hspace{1cm} \text{// just reorder the elements in the sum} \\
&= (\Delta m_0 + e_0) + (\Delta m_1 + e_1)\cdot X + (\Delta m_2 + e_2)\cdot X^2 + (\Delta m_3 + e_3)\cdot X^3
\end{aligned}
$$

This means that by computing $(b_0 - a_0 {\color{red} s_0} + a_3 {\color{green} s_1} + a_2 {\color{orange} s_2} + a_1 {\color{cyan} s_3})$ (followed by rescaling by $\Delta$ and rounding), we decrypt the coefficient $m_0$. In the same way, by computing $(b_1 - a_0 {\color{green} s_1} - a_1 {\color{red} s_0} + a_2 {\color{cyan} s_3} + a_3 {\color{orange} s_2})$ (followed by rescaling by $\Delta$ and rounding), we decrypt the coefficient $m_1$, and so on for all coefficients.

Starting from this observation we can build LWE ciphertexts encrypting all the coefficients of the RLWE input ciphertext separately, under the extracted secret key $\vec{s} = ({\color{red} s_0}, {\color{green} s_1}, {\color{orange} s_2}, {\color{cyan} s_3})$, as follows:
$$
\begin{cases}
(a_0, - a_3, - a_2, - a_1, b_0) &\in LWE_{\vec{s}, \sigma}(\Delta m_0) \subseteq \mathbb{Z}_q^{n+1} \\
(a_1 , a_0, - a_3, - a_2, b_1) &\in LWE_{\vec{s}, \sigma}(\Delta m_1) \subseteq \mathbb{Z}_q^{n+1} \\
(a_2, a_1, a_0, - a_3, b_2) &\in LWE_{\vec{s}, \sigma}(\Delta m_2) \subseteq \mathbb{Z}_q^{n+1} \\
(a_3, a_2, a_1, a_0, b_3) &\in LWE_{\vec{s}, \sigma}(\Delta m_3) \subseteq \mathbb{Z}_q^{n+1} \\
\end{cases}
$$

Blind Rotation

The third and last building block is the core of the bootstrapping. It is called blind rotation because it realizes a rotation of the coefficients of a polynomial in a blind way, meaning that we will rotate the coefficients but the number of rotated position is encrypted. Let's go there step by step.

First of all, what does it mean to rotate the coefficients of a polynomial and how do we do that? It simply means that we want to shift the coefficients towards the left (or the right), and to do so, we simply multiply the polynomial by a monomial $X^{-\pi}$ (or $X^{\pi}$), where $0 \leq \pi < N$ is the number of positions we want to rotate. If we take as input a polynomial:
$$
M = m_0 + m_1 X + m_2 X^2 + \ldots + m_\pi X^\pi + \ldots + m_{N-1} X^{N-1} \in \mathcal{R}_q
$$
and we multiply it times $X^{-\pi}$ in $\mathcal{R}_q$, we obtain what follows:
$$
M \cdot X^{-\pi} = m_{\pi} + m_{\pi+1} X + \ldots + m_{N-1} X^{N-\pi-1} - m_0 X^{N-\pi} - \ldots - m_{\pi-1} X^{N-1} \in \mathcal{R}_q.
$$
In practice, the rotation was able to bring the coefficient that originally was in position $\pi$ down to the constant coefficient position. Of course, since the rotation is computed modulo $X^N + 1$, the coefficients from $m_0$ to $m_{\pi-1}$ passed "on the other side" with a minus sign.

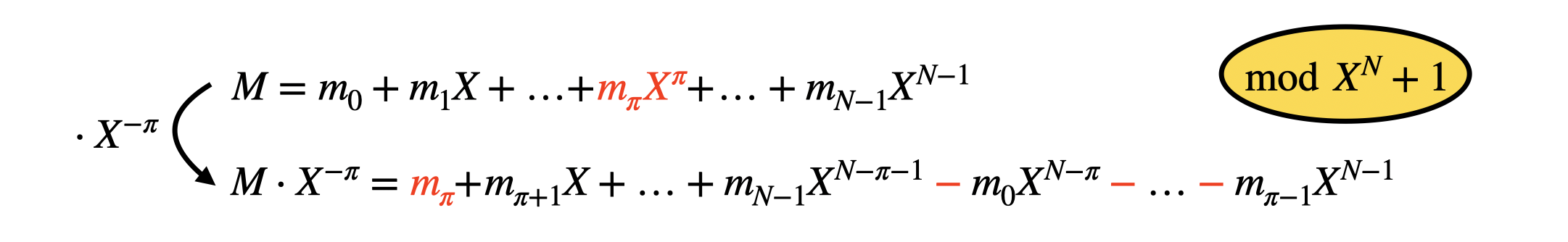
Let's now add a little bit of difficulty and let's try to rotate an encrypted polynomial of $\pi$ positions. In TFHE, we can encrypt polynomials with GLWE ciphertexts: the rotation is performed by simply rotating all the components of the GLWE by multiplying them times $X^{-\pi}$. If we have in input the GLWE ciphertext:
$$
C = \left(A_0, \ldots, A_{k-1}, B \right) \in GLWE_{\vec{S}, \sigma}(\Delta M) \subseteq \mathcal{R}_q^{k+1}
$$
the rotation is performed as follows:
$$
C^{(\mathsf{rot})} = \left(A_0 \cdot X^{-\pi}, \ldots, A_{k-1} \cdot X^{-\pi}, B \cdot X^{-\pi} \right) \in GLWE_{\vec{S}, \sigma}(\Delta M \cdot X^{-\pi}) \subseteq \mathcal{R}_q^{k+1}.
$$
The result is then a GLWE ciphertext encrypting the rotated message polynomial $M \cdot X^{-\pi} \in \mathcal{R}_p$. Observe that this operation does not increase the noise.

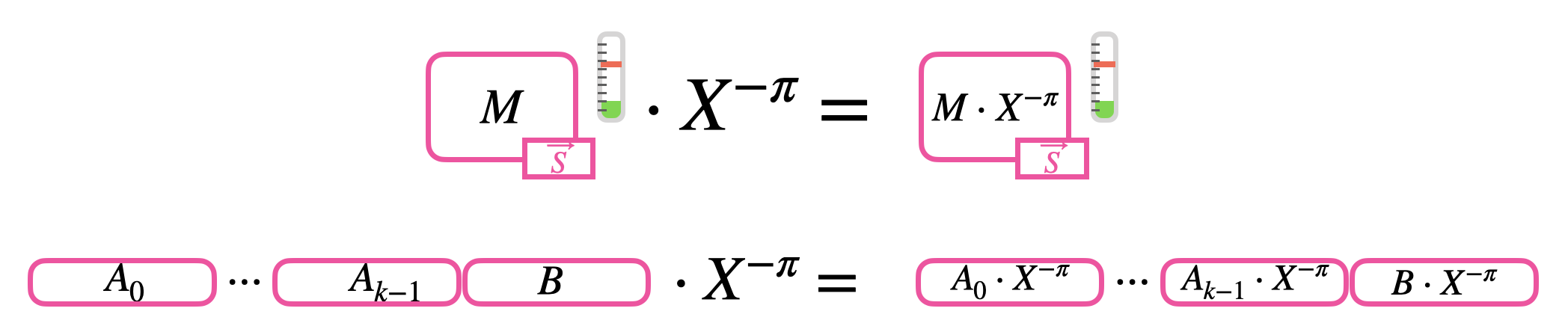
Let's add the final level of difficulty, which is the encryption of the value $\pi$ to finally make a blind rotation. To do so, in TFHE, we use iteratively the CMux operation, described at the end of the previous blogpost. Recall that the CMux operation takes in input two GLWE ciphertexts encrypting the two options and a GGSW ciphertext encrypting the selection bit. The value of $\pi$ will be used as the selection in our construction. However $\pi$ is an integer value, so we need to express it in its binary decomposition:
$$
\pi = \pi_0 + \pi_1 \cdot 2 + \pi_2 \cdot 2^2 + \ldots + \pi_\delta \cdot 2^\delta
$$
where $\delta = \log_2(N)$. What we want to compute is:
$$
\begin{aligned}
M \cdot X^{-\pi}
&= M \cdot X^{-\pi_0 -\pi_1 \cdot 2 -\pi_2 \cdot 2^2 + \ldots -\pi_\delta \cdot 2^\delta} \\
&= M \cdot X^{-\pi_0} \cdot X^{-\pi_1 \cdot 2} \cdot X^{-\pi_2 \cdot 2^2} \cdot \ldots \cdot X^{-\pi_\delta \cdot 2^\delta}. \\
\end{aligned}
$$
Let's take a generic monomial $X^{-\pi_j \cdot 2^j}$ and let's try to understand how to perform the computation homomorphically. Observe that, since $\pi_j$ is binary, two options are possible when we compute $M \cdot X^{-\pi_j \cdot 2^j}$:
$$
M \cdot X^{-\pi_j \cdot 2^j} =
\begin{cases}
M &\text{ if } \pi_j = 0 \\
M \cdot X^{-2^j} &\text{ if } \pi_j = 1 \\
\end{cases}
$$
This is exactly an if condition, and we have seen that we can evaluate it as a CMux that takes as inputs:

• a GGSW encryption of $\pi_j$ as selector;
• a GLWE encryption of $M$ as the "0" option;
• a GLWE encryption of $M$ times $X^{-2^j}$ (rotation of a clear number of positions) as the "1" option.

The result of this operation is a GLWE encryption of $M \cdot X^{-\pi_j \cdot 2^j}$ as we wanted.

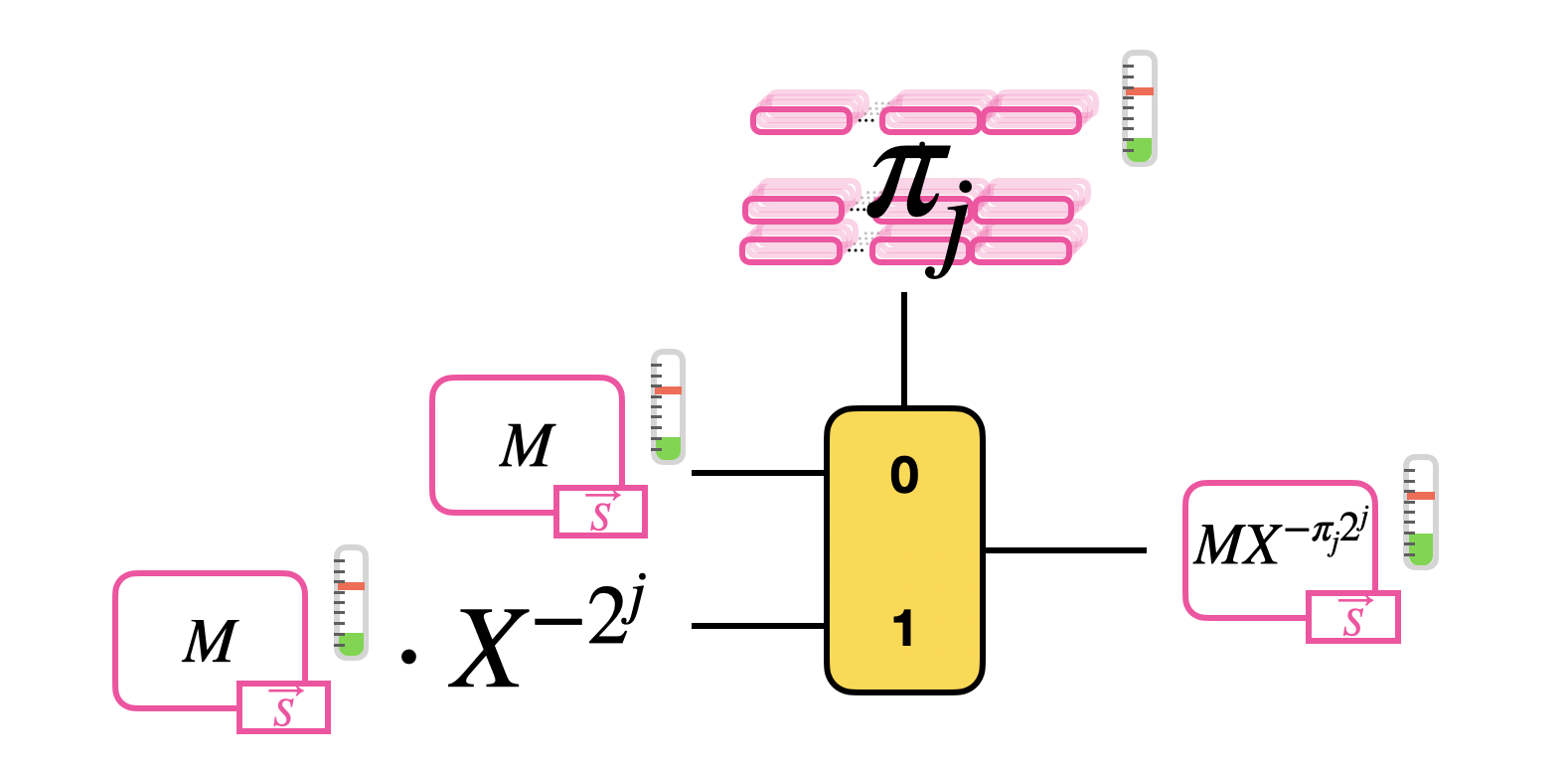
Than, the blind rotation computes recursively the product of the GLWE encryption of $M$ by each of these monomials, so it performs a sequence of $\delta$ CMuxes. The result of a CMux becomes the new message option of the following CMux.

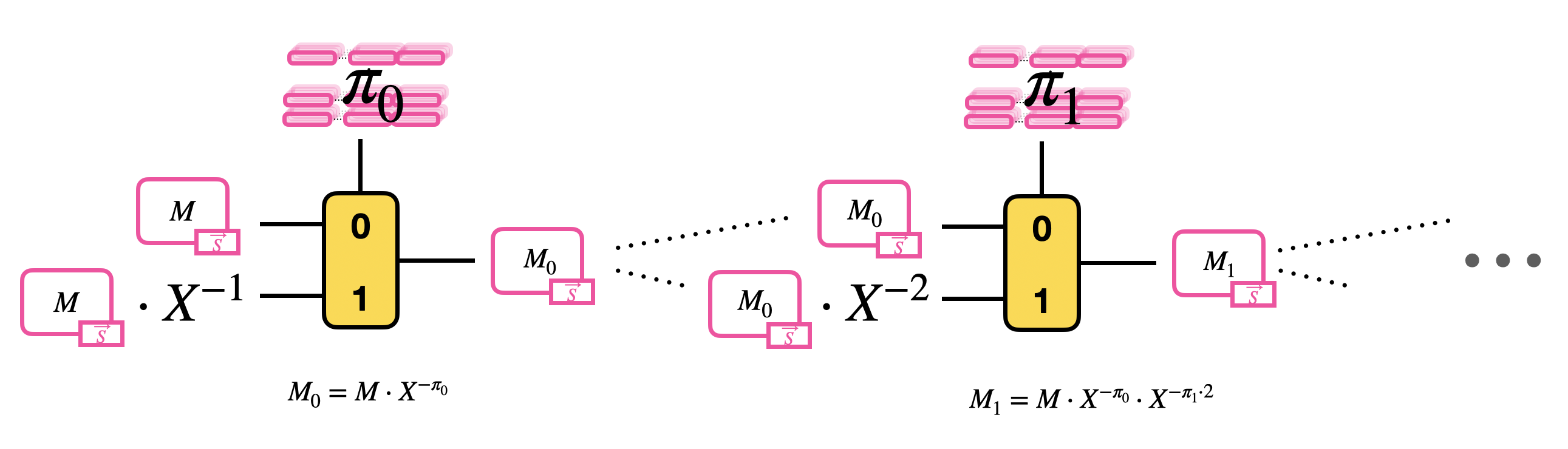
Bootstrapping

We are finally ready to build bootstrapping!  

Bootstrapping is an operation introduced in 2009 by Gentry, allowing to reduce noise and so to build homomorphic functions (potentially) as large as we want. However, even if bootstrapping has been the ultimate solution to the noise problems in FHE, it still remains one of the most costly homomorphic operations, both in terms of memory consumption and computational cost. For this reason, in the last decade the research in FHE has tried to improve this operation as much as possible.

Since the goal of bootstrapping is to reduce the noise in ciphertexts, the way to go is to evaluate the decryption function homomorphically. In fact, decryption is the only operation that is really able to get rid of all the randomness, and especially the noise.

The bootstrapping in TFHE acts on LWE ciphertexts, so tuples $c = (a_0, \ldots, a_{n-1}, b) \in LWE_{\vec{s}, \sigma}(\Delta m) \subseteq \mathbb{Z}_q^{n+1}$, encrypting a message $m \in \mathbb{Z}_p$ under the secret key $\vec{s} = (s_0, \ldots, s_{n-1}) \in \mathbb{Z}^n$. Recall that the LWE decryption consists in two steps:

1. The computation of the linear combination $b-\sum_{i=0}^{n-1} a_i s_i = \Delta m + e \in \mathbb{Z}_q$;
2. The rescale and rounding $\left\lfloor \frac{\Delta m + e}{\Delta} \right\rceil = m$.

Now the question is, by using all the building blocks we introduced in this series of blog posts, how can we evaluate these two operations homomorphically and be able to reduce noise?

The TFHE approach is to put the computation of (the negation of) $b-\sum_{i=0}^{n-1} a_i s_i = \Delta m + e$ in the exponent of a monomial $X$, and then to use this new monomial to rotate a Look-Up Table (LUT) that evaluates the second step of the decryption (rescale and rounding).

Well, this seems easy to say but the devil is in the details: so let's dig into it! We will actually start from step 2, so for a moment we assume we have already computed $X^{-(\Delta m + e)}$.

Step 2

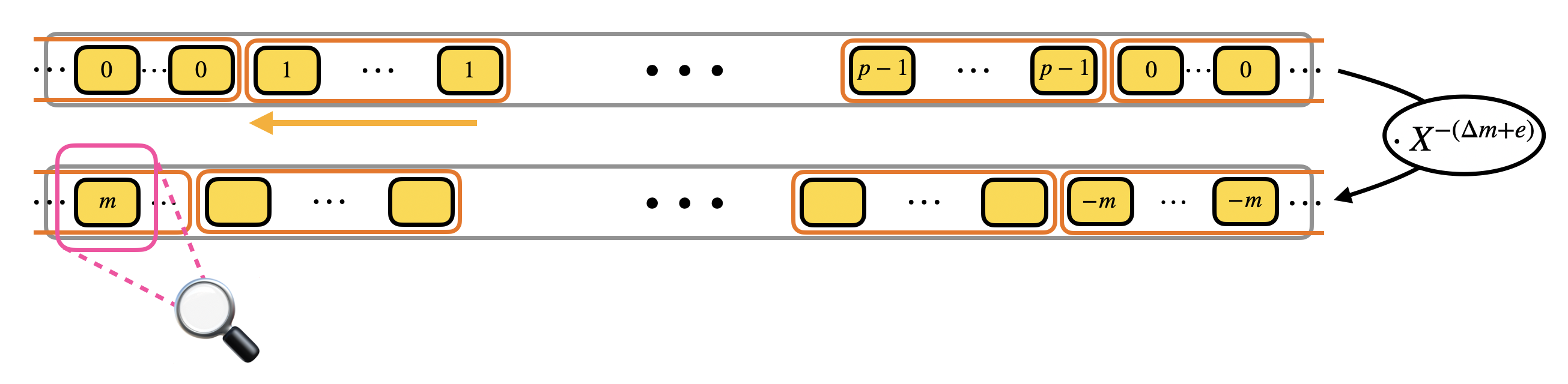
If you want to perform the rescale and round you want to be able to associate the value $m$ to the value $\Delta m + e$, whatever the value of $e$ is, under the only necessary condition for correct decryption that $|e| < \Delta/2$ (as we have seen in the first blog post). The value of $\Delta m + e$ is in $\mathbb{Z}_q$, while $m$ is in $\mathbb{Z}_p$, with $p<q$. So this means that there will be repetitions: as instance if the message is $m$, the values $\Delta m$, $\Delta m + 1$, $\Delta m - 1$, etc., will be all sent to $m$. We try to give you the intuition in the following figure.

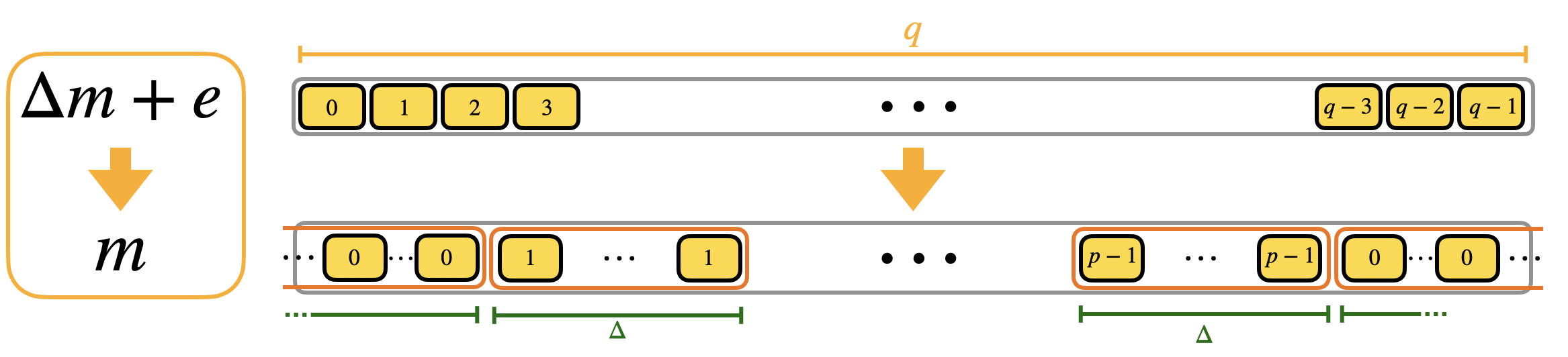
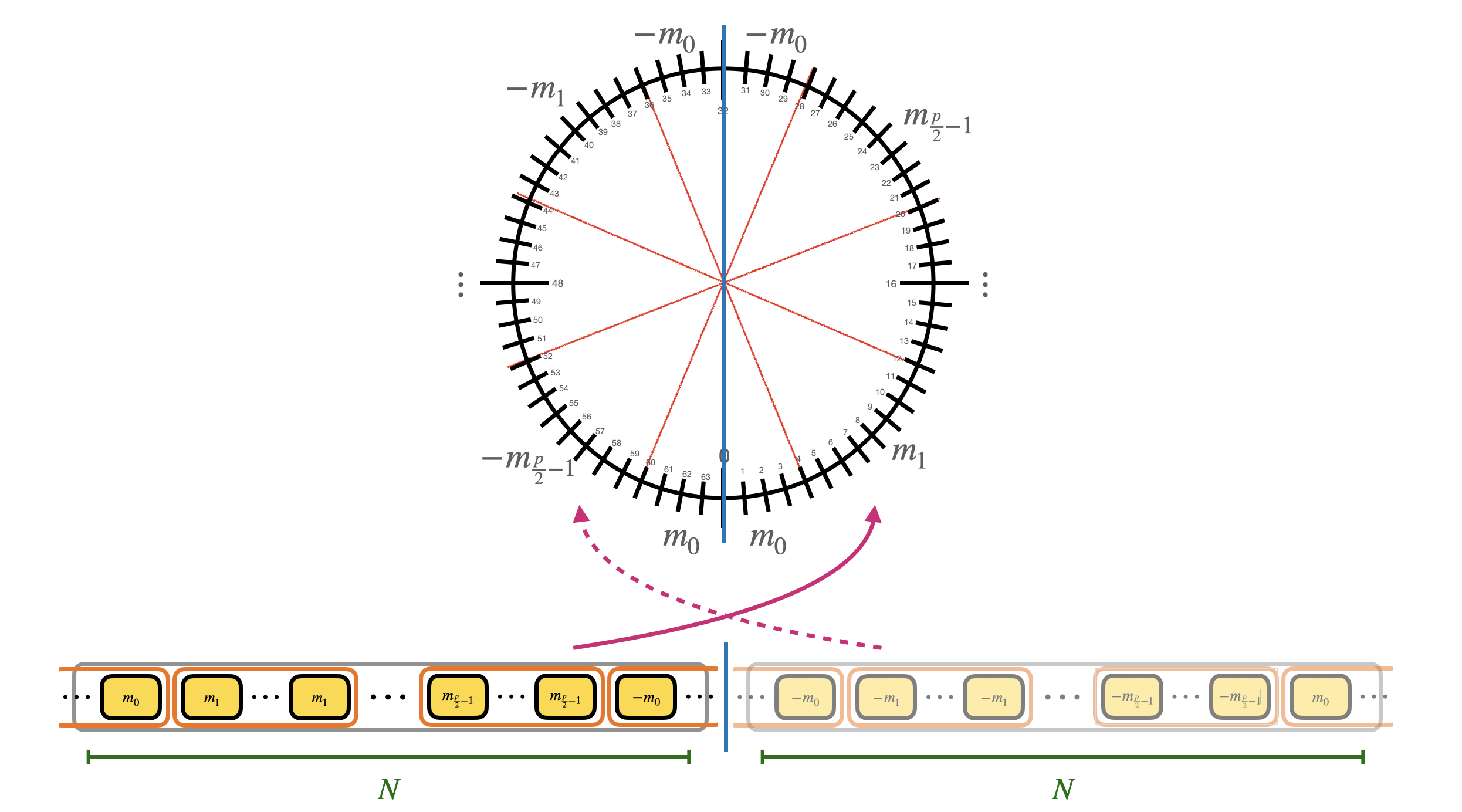
We call the blocks containing multiple repetitions of the same value mega-cases. Observe that the mega-case corresponding to the value $0$ is split into 2 halves, cause if the error is negative, then $\Delta 0 + e$ is a negative value and goes up to $q-1$, $q-2$ and so on (modulo $q$). We actually already shown the mega-cases in the second blog post when we presented the torus representation. Here is a figure with a toy example to see the correspondence.

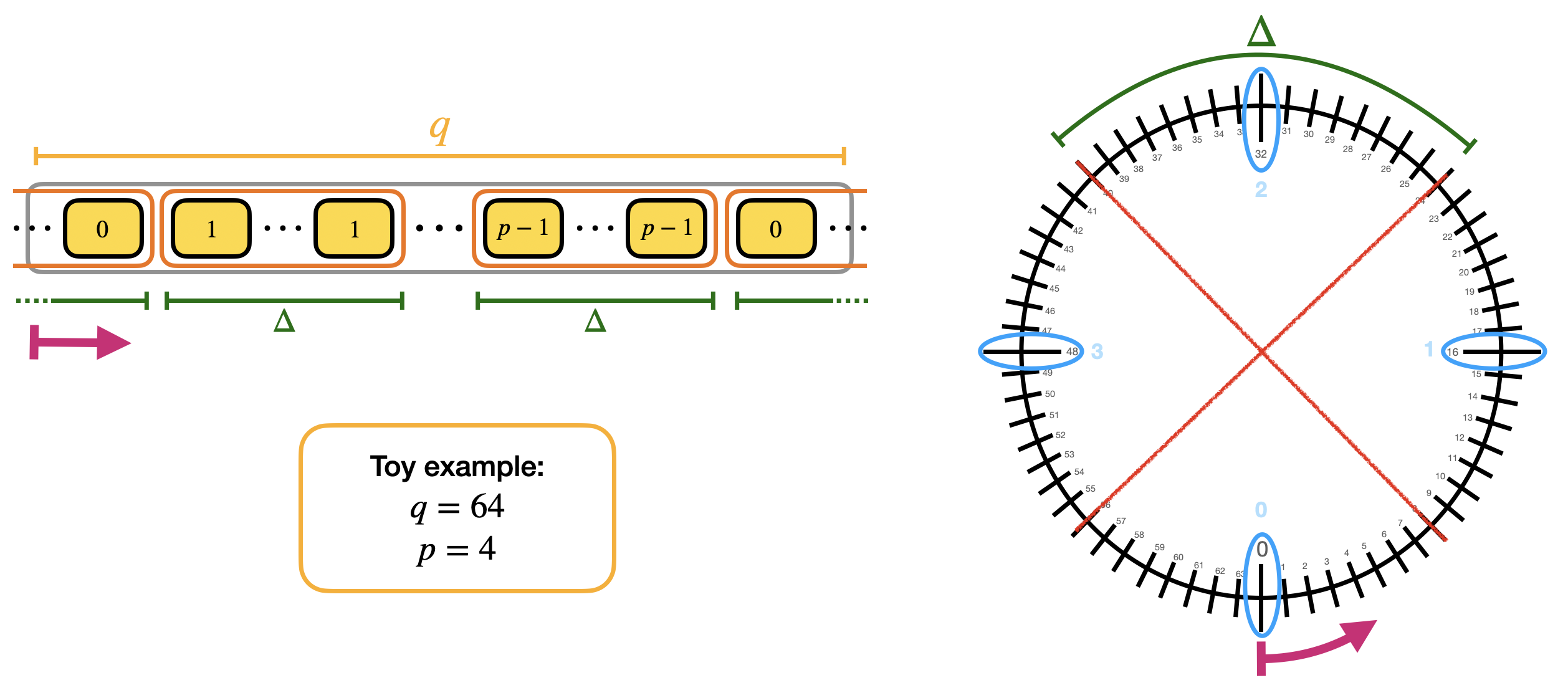
The way we evaluate such LUT is by performing a polynomial rotation: the idea is to put all the elements of the redundant LUT into a polynomial and rotate the polynomial of $\Delta m + e$ positions by multiplying it times $X^{-(\Delta m + e)}$. The rotation has the effect to bring one of the elements contained in the mega-case corresponding to $m$ in the constant position of the polynomial. For us the constant position of polynomials can be considered as the reading position: so when we want to read a coefficient of a polynomial, we rotate the polynomial until the coefficient is in constant position instead of going to the coefficient location.

Now it is important to notice that the polynomials we manipulate in TFHE are polynomials modulo $X^N + 1$, so they can contain only $N$ coefficients. In practice $N$ is way smaller than $q$ (an example of practical parameters is $N=2^{10}$ and $q=2^{32}$), so we need to find a way to compress the information modulo $q$ to a space that is way smaller: for this we will use the modulus switching that we presented in the previous paragraphs.

Furthermore, the monomial $X$ modulo $X^N+1$ has order $2N$, which in practice means that to get back the identity we need to rotate times $X^{2N}$ (in fact $X^N \equiv -1$ and $X^{2N} \equiv 1$). This means that, by fixing the $N$ coefficients of the polynomial, we are actually fixing $2N$ coefficients: the second half is a copy of the first $N$ coefficients with opposite sign. This is called negacyclic property: if the LUT you are evaluating is negacyclic, then you can encode the information by using all the $p$ possible values for the message, otherwise, you can only use $\frac{p}{2}$. In practice, this means that to bootstrap with a non negacyclic LUT, we need to use a bit of padding in the encoding of the message (for encodings, double check the second blog post). The modulus switching is going to be done from $q$ to $2N$.

Step 1

Now that we have an intuition on how to evaluate the second step of decryption, let's go back to the first step: the homomorphic computation of $X^{-(\Delta m + e)}$. Recall that to be able to rotate we need to compress message information from modulo $q$ to modulo $2N$ via modulus switching:
$$
c = (a_0, \ldots, a_{n-1}, b) \in LWE_{\vec{s}, \sigma}(\Delta m) \subseteq \mathbb{Z}_q^{n+1} \longmapsto \tilde{c} = (\tilde{a}_0, \ldots, \tilde{a}_{n-1}, \tilde{b}) \in LWE_{\vec{s}, \sigma'}(\tilde{\Delta} m) \subseteq \mathbb{Z}_{2N}^{n+1}
$$
Once this step is done, we use the output of the modulus switching to put the information in the exponent of $X$. This is done by performing a blind rotation, taking as input a trivial GLWE encryption of the LUT polynomial, that we will note by $V$, all the elements of $ \tilde{c} = (\tilde{a}_0, \ldots, \tilde{a}_{n-1}, \tilde{b})$ and GGSW encryptions of the LWE secret key elements $\vec{s} = (s_0, \ldots, s_{n-1})$ under a new GLWE secret key $\vec{S}'$. These GGSW encryptions of the secret key elements are what we call the bootstrapping key.

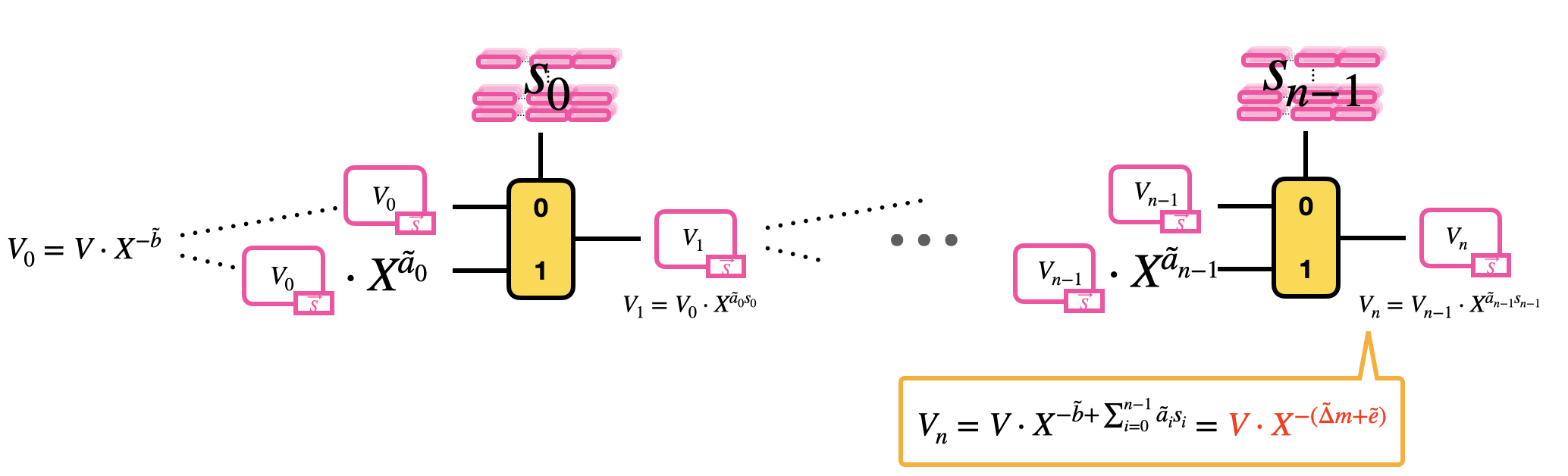
The blind rotation is done as follows:

• Initialize the blind rotation by multiplying the trivial GLWE encryption of $V$ times $X^{-\tilde{b}}$ (rotation);
• Pass the trivial encryption of $V\cdot X^{-\tilde{b}} = V_0$ as input to a first CMux: the CMux uses as selector the GGSW encryption of the bit $s_0$ of the LWE secret key, and as options $V_0$ and $V_0 \cdot X^{\tilde{a}_0}$. This step outputs a GLWE encryption of $V_1 = V_0 \cdot X^{\tilde{a}_0 s_0}$.
• Pass the GLWE encryption of $V_1$ to a second CMux: the CMux uses as selector the GGSW encryption of the bit $s_1$ of the LWE secret key, and as options $V_1$ and $V_1 \cdot X^{\tilde{a}_1}$. And so on until a total of $n$ CMuxes.

The result of this blind rotation is a GLWE encryption of
$$
\begin{aligned}
V_n
&= V_{n-1} \cdot X^{\tilde{a}_{n-1} s_{n-1}} \\
&= \ldots \\
&= V \cdot X^{-\tilde{b}} \cdot X^{\tilde{a}_0 s_0} \cdot \ldots \cdot X^{\tilde{a}_{n-1} s_{n-1}} \\
&= V \cdot X^{-\tilde{b} + \sum_{i=0}^{n-1} \tilde{a}_i s_i} = V \cdot X^{-(\tilde{\Delta} m + \tilde{e})} \\
\end{aligned}
$$

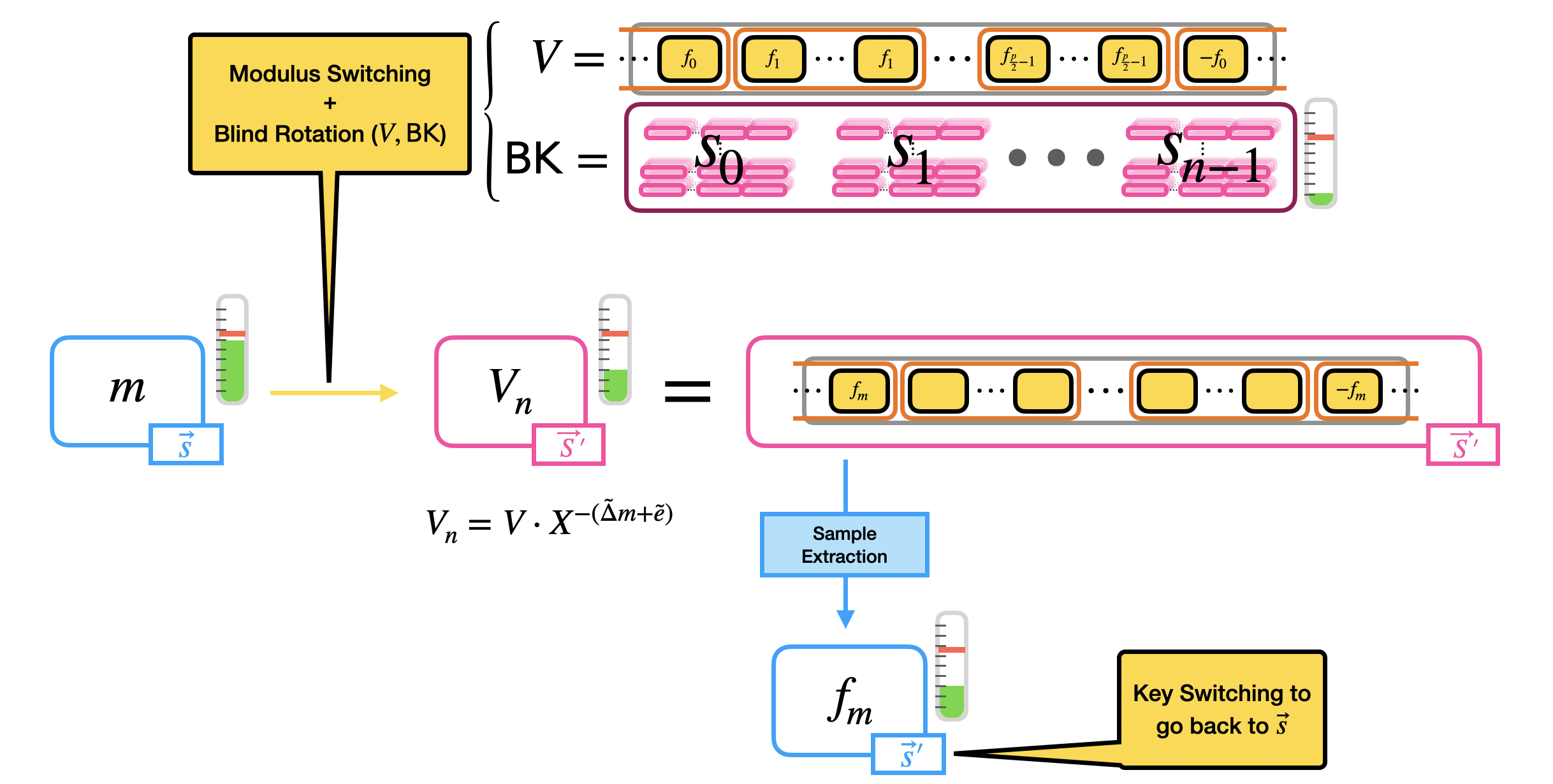
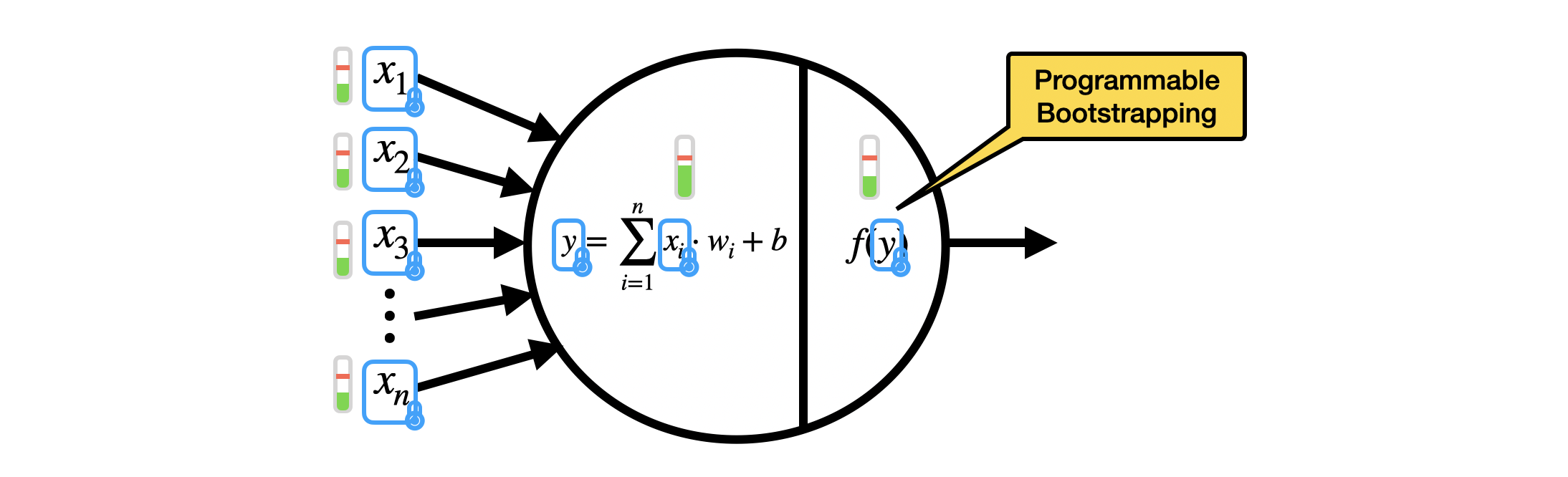
Putting Things Together

We are almost done: the last step of the bootstrapping is a sample extraction. The result of the blind rotation is in fact a GLWE encryption of $V \cdot X^{-(\tilde{\Delta} m + \tilde{e})}$ which, by construction of $V$ in Step 1, is a polynomial whose constant coefficient is one of the elements of the mega-case corresponding to $m$. As we said, the constant coefficient is our reading position, and the way we "homomorphically read" what is inside the constant coefficient is by extracting it as an LWE ciphertext via sample extraction.

A few more observations before we summarize:

• The blind rotation evaluates a LUT encoded inside the polynomial $V$. Until now we said that the output for bootstrapping is an encryption of $m$ and we encoded this value on $V$. But the LUT can actually encode any function evaluated on the inputs. So if instead of putting $m$ in $V$, we put $f_m$, where $f_m$ is the output of a function $f$ evaluated on $m$, then the bootstrapping is able to evaluate the function $f$ at the same time as it reduces the noise. This is why it is very often called programmable bootstrapping. Observe that the value $m$ is a special case of $f_m$, where the function is the identity. Whatever the value of $f_m$ is, we generally put a scaling factor in front of it, that could be the same as the original scaling factor $\Delta$ or a new one (so in $V$ we have values $\Delta' f_m$). Observe also that evaluating the bootstrapping that simply refreshes the noise or the bootstrapping that evaluates any LUT have exactly the same cost.
• The polynomial $V$ is generally given un-encrypted (we pass to the bootstrapping a trivial GLWE encryption of $V$). However, if we want to hide the LUT we are evaluating, we can give in input to bootstrapping the polynomial $V$ encrypted as a (non trivial) GLWE ciphertext. This has a minimal impact on the noise and provides the additional functionality of function hiding with almost no impact on performances.
• Some might observe that, thanks to the way TFHE bootstrapping is build, we are able to get rid of the input noise. However, bootstrapping consists in a bunch of homomorphic operations that, by definition, make the noise grow again. The trick comes from the bootstrapping keys: they are chosen with parameters that allow the noise to be very small (all by keeping the security level), so that after the bootstrapping computations the output noise is way smaller than the noise in the input LWE ciphertext. A wrong choice of parameters can of course compromise the result: that is why a good choice of parameters is fundamental for bootstrapping to work successfully. The choice of parameters is still one of the hardest tasks in FHE, but this is not the focus of these blog posts.

To summarize, the bootstrapping of TFHE takes as input an LWE ciphertext $c = (a_0, \ldots, a_{n-1}, b) \in LWE_{\vec{s}, \sigma}(\Delta m) \subseteq \mathbb{Z}_q^{n+1}$, a polynomial $V \in \mathcal{R}_q$ and a bootstrapping key $\mathsf{BK} = (\mathsf{BK}_0, \ldots, \mathsf{BK}_{n-1})$, where $\mathsf{BK}_i \in GGSW^{\beta, \ell}_{\vec{S}', \sigma}(s_i) \subseteq \mathcal{R}_q^{(k+1) \times \ell (k+1)}$ is a GGSW encryption of the secret LWE key bit $s_i$ under the GLWE secret key $\vec{S}'$. Then, the bootstrapping does the following steps:

1. Modulus switching: on the input LWE ciphertext $c$ to switch from modulo $q$ to modulo $2N$, giving in output $\tilde{c} = (\tilde{a}_0, \ldots, \tilde{a}_{n-1}, \tilde{b}) \in LWE_{\vec{s}, \sigma'}(\tilde{\Delta} m) \subseteq \mathbb{Z}_{2N}^{n+1}$;
2. Blind rotation: on the polynomial $V$ (encrypted as a trivial GLWE ciphertext) by using the output LWE ciphertext of modulus switching $\tilde{c}$ and the bootstrapping key $\mathsf{BK}$, giving in output a GLWE encryption of $V \cdot X^{-(\tilde{\Delta} m + \tilde{e})}$ under a new GLWE secret key $\vec{S}'$;
3. Sample extraction: of the constant coefficient of the GLWE output of the blind rotation, as a LWE encryption of $f_m$, under the extracted LWE secret key $\vec{s}'$.
   

Observe that if you want to go back from the new LWE secret key $\vec{s}'$ to the original LWE secret key $\vec{s}$, an LWE-to-LWE key switching can be performed (for key switching we refer to the third blog post). The image below summarizes the bootstrapping.

An example of bootstrapping: the Gate Bootstrapping

Before we conclude, let us cite a very famous example of bootstrapping used in TFHE: the gate bootstrapping.Gate bootstrapping is called this way because it evaluates a binary gate operation homomorphically and reduces the noise at the same time. All the binary gates can be evaluated (AND, NAND, OR, XOR, etc.) but we can focus here on the AND gate, just to make the example.

The gate bootstrapping takes as input two LWE ciphertexts $c_1, c_2$, encrypting two bits $\mu_1, \mu_2$ under the same secret key. The bit information is encoded in a special way: $0$ is encoded as $-q/8$ while $1$ is encoded as $q/8$. Then the operation works in two steps:

• We start by making a linear combination the two ciphertexts (the linear combination depends on the gate evaluated). If we need to add a constant, we use the addition by constant described in the second blog post.
• We perform a bootstrapping (followed by a key switching to bring back the original key) that evaluates the LUT encoded in the polynomial $V = \sum_{j=0}^{N-1} \frac{q}{8} X^j$. This is a sort of rescaled sign function, that outputs $\frac{q}{8}$ to all the messages with positive sign, and $-\frac{q}{8}$ to all the messages with negative sign. This is a negacyclic function so no need for a bit of padding.

The table makes all the steps explicit, by showing the encoding, the result of the linear combination and the bootstrapping. The last columns shows that the encoding corresponds to the correct output.

The next figure gives the visual representation of the bootstrapping function.

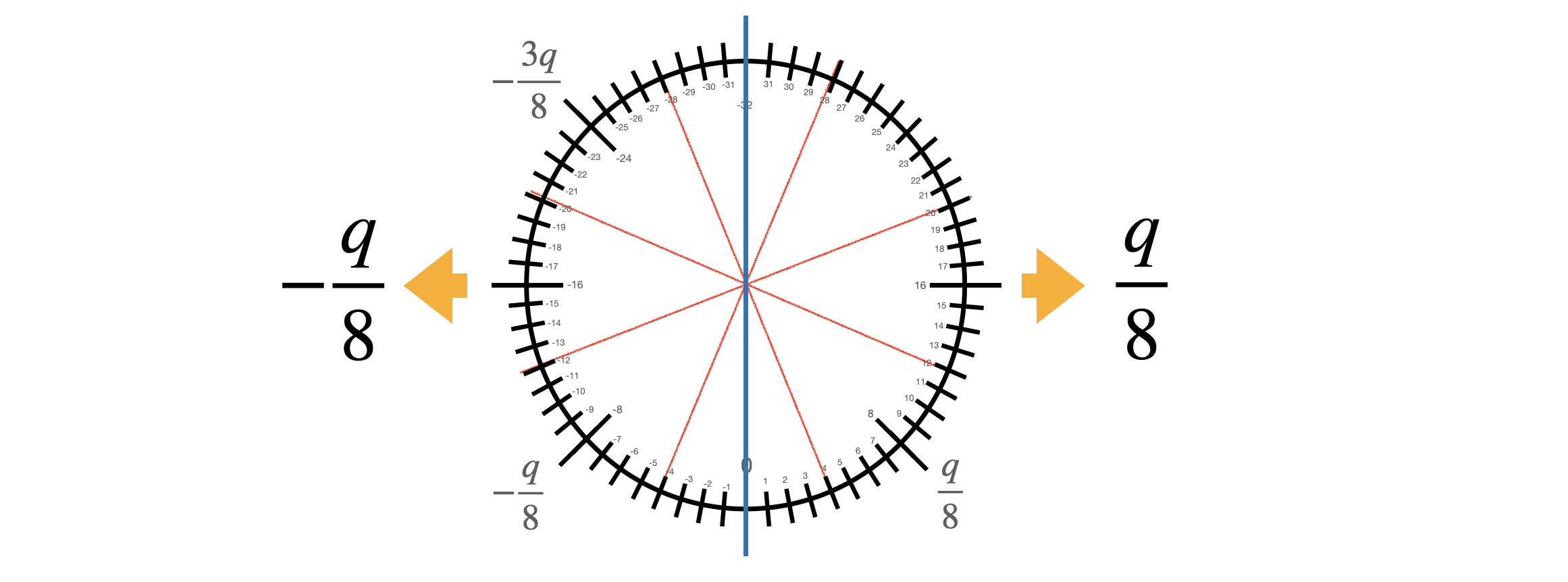
What is nice in gate bootstrapping is that the output has the same encoding as the inputs and the noise level that has been reduced by the bootstrapping, so it is ready to be passed as input to the following Boolean gate.

An example of bootstrapping: Neural Networks applications

One of the major applications of TFHE is the homomorphic evaluation of the inference of artificial Neural Networks (NN). A NN is composed of artificial neurons. In the simplest neural networks, the neurons take as input the integer outputs of previous neurons $(x_1, \ldots, x_n)$ (or the inputs to the NN, if the neurons are at the first layer), and evaluate the neuron in two steps:

• A linear combination between the integer inputs $(x_1, \ldots, x_n)$ times given integer weights $(w_1, \ldots, w_n)$, plus an integer bias $b$: this outputs an integer $y = \sum_{i=1}^{n} x_i w_i + b$;
• An activation function $f$ evaluated on $y$: an activation function is a non-linear function, such as the sign function, ReLU, sigmoid, hyperbolic tangent, and so on.
  

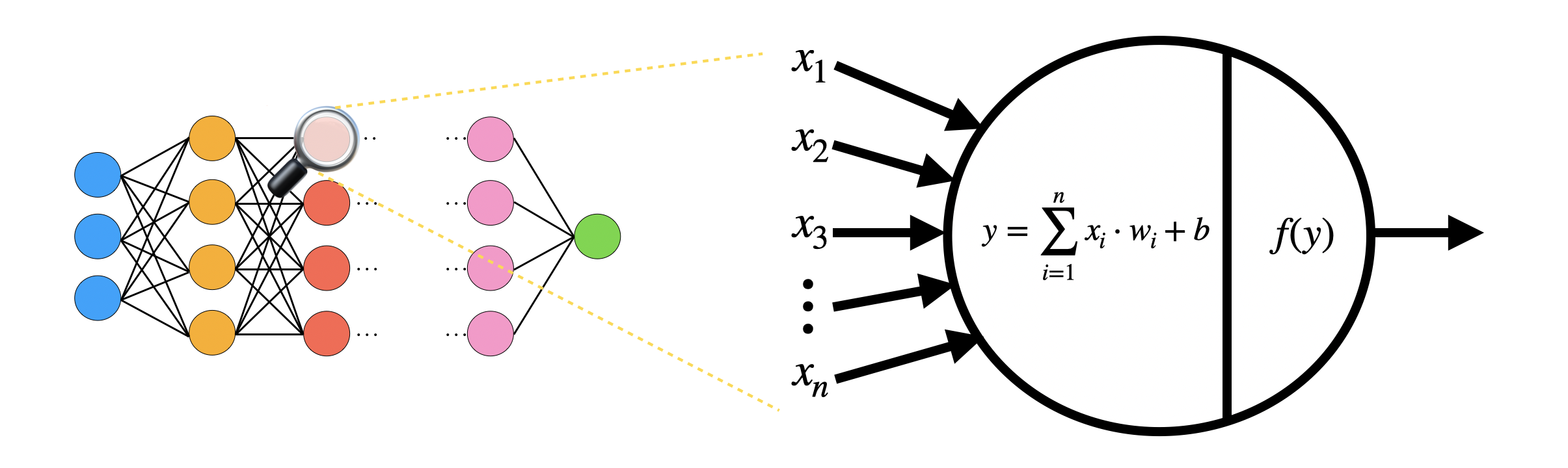
In TFHE, we can evaluate the inference of NN homomorphically, by encrypting the integer inputs $x_i$ (up to about $8$ bits) as LWE ciphertexts. We evaluate the linear combination as a list of multiplications between LWE ciphertexts and constants, and LWE additions. The activation function is evaluated as a programmable bootstrapping, so the noise is reduced at the same time and the output can be passed to the next neuron. Since noise is managed inside each neuron, we can potentially evaluate any NN, even very deep ones. We refer to this paper for some experimental results.

We arrived to the end of this series of blog posts dedicated to TFHE. If you arrived until here, congratulations!
‍
The scheme offers way more features than the ones we presented here: another series of blog posts would be necessary to get even deeper in the understanding of the scheme and its advanced modes. In the meantime, if you want to play in practice with TFHE, do not hesitate to check the TFHE-rs (we're open source) and give us a star:

‍

In any case, we hope that you enjoyed the reading and that you learned more about the scheme. Thank you for taking the time!
And a special thank you to Damien Ligier, Jean-Baptiste Orfila and Samuel Tap for the valuable feedback and editing of this blog post.

Additional links

• ⭐️ Like our work? Support us and star TFHE-rs on Github
• 👋 Questions? Join the Zama community.
• 💸 Join the Zama Bounty Program. Solve FHE problems, write tutorials and earn rewards, more than €500,000 in prizes.