HPU Deepdive: How FHE Operations Run on the Homomorphic Processor

Introduction

The Homomorphic Processing Unit (HPU) is a hardware accelerator designed by Zama to perform computations directly on encrypted data. It provides an accessible user interface, while relying on tfhe-rs as the cryptographic reference software with TFHE (Fully Homomorphic Encryption over Torus) scheme. (If you’d like a gentle mathematical introduction to TFHE, we recommend this excellent deep dive post)

In this article, we’ll explain how the HPU executes an operation. The goal is to give curious developers a clear mental model for using the HPU—and, for the brave, to dive into its RTL code.

Of course, hardware never works alone. The HPU project also includes a software stack:

• Driver
• DMA access tools
• tfhe-rs + HPU backend for pre- and post-processing

These components run on the host CPU, which manages the interaction with the HPU. In this post, we’ll focus on the hardware side, and only briefly mention the software where relevant. If you’re interested in the software implementation details, refer to GitHub.

Specifications

Before diving into the hardware details, let’s clarify what the HPU actually is and how it works.

The HPU is a PCIe companion chip that operates alongside a host CPU (simply called “the host” here). The roles are clearly split:

• The host prepares the ciphertexts and cryptographic keys, starts computations, and retrieves the results.
• The HPU focuses exclusively on computations over ciphertexts. It cannot encrypt or decrypt data on its own.

To make this interaction possible, a dedicated protocol manages communication between the host and the HPU.

Integer representation

The HPU follows the same radix representation as tfhe-rs. Why? Because encrypting full integers directly in FHE/TFHE would make ciphertexts huge—growing exponentially with integer size—and computations would quickly become impractical.

Instead, integers are split into digits, and each digit is encrypted separately. These smaller digit ciphertexts are also called elementary ciphertexts.

Encrypting each digit ciphertext is much smaller than encrypting the entire integer directly. Even the full set of digit ciphertexts is still smaller than a single “whole integer” ciphertext. The trade-off is that computations involve more elementary steps, but this cost is far outweighed by the efficiency gained from reduced ciphertext size.

Elementary ciphertexts

Think of an elementary ciphertext as a word of b bits. In practice, tfhe-rs uses ciphertexts encoding 4 bits plus d 1 padding bit (this latter is needed for the negacyclic property of polynomials—see the TFHE-rs handbook for details).

In the current HPU version:

• Each integer is decomposed into 2-bit digits (“message” part).
• The remaining 2 bits in the 4-bit part are reserved for computation (“carry” part).

Computations on the HPU

The HPU is a programmable processing unit, meaning it runs programs provided by the user. Since the computations in the HPU operate on elementary ciphertexts at the digit level, the instructions are naturally expressed as digit operations (DOp).

Writing DOp directly can be tricky, especially for users who think in the perspective of full integers. To simplify this, the HPU can automatically translate integer operations (IOp) into the corresponding DOp code. In practice:

• Developers usually provide high-level IOp code.
• The HPU translates it into the low-level DOp code it can execute.
• Common IOps already come with pre-defined DOp programs.
• For custom IOps, users can still define their own DOp and hand it to the HPU.

To make this easier, the HPU backend includes tools for writing and testing these codes.

What makes the HPU different from a regular CPU?

At first glance, the HPU looks like a simple CPU: it loads instructions, processes data, and produces results. The difference lies in what it computes on: instead of plain 16-, 32-, or 64-bit integers, the HPU works on FHE ciphertexts.

Ciphertexts, however, bring an additional challenge: noise.

• In TFHE, ciphertexts carry noise. As long as the noise stays below a threshold, the plaintext can still be correctly recovered.
• Each homomorphic operation increases noise. Too much noise, and the ciphertext becomes unusable.

This is where Bootstrapping (BS) comes in.

• Bootstrapping “refreshes” a ciphertext by reducing its noise, enabling further operations.
• TFHE extends this idea with Programmable Bootstrapping (PBS), which not only cleans the ciphertext but can also apply a Look-Up Table (LUT) to the value—for free.

Another crucial step is Key Switching (KS), which reformats ciphertexts so they can be processed correctly by PBS.

The HPU implements both KS and PBS directly in hardware. This makes it possible to perform an unlimited number of computations on TFHE ciphertexts. In fact, one of the available DOp instructions is precisely KS + PBS.

‍

Example: Computing |A – B|

The first step to using the HPU is defining the IOp you want, and if necessary, providing its DOp implementation. Once that’s done, the HPU takes care of execution—noise management, LUT application, and parallel dispatch included.

Let’s walk through a concrete example step by step.

1. Writing the code

Suppose a user wants to compute the absolute difference between two encrypted values R=∣A−B∣ where A and B are two 2-bit ciphertexts encrypted with TFHE.

If this operation (IOp) is not already available in the catalogue, the user must define a custom IOp. Its signature is the following:

IOP[0x01] <I2 I2> <I2@0x0> <I2@0x4 I2@0x8>

Here, this signature means. In details:

• IOP[0x01]: Defines a custom integer operation with the identifier 0X01
• <I2 I2>: Specifies alignment rules in memory for ciphertext addresses.
• <I2@0x0>: Specifies the destination address offset where the results will be stored
• <I2@0x4 I2@0x8>: Specifies the inputs.
  
  • I2@0x4: first input (A) stored at address offset 0x4.
  • I2@0x8: second input (B) stored at address offset 0x8
    

(Full IOp syntax: docs)

At the pseudocode level, the operation looks like this:

# Input: A, B elementary ciphertexts.
# Output: R = |A-B|, which is an elementary ciphertext.
SEL = A > B # Boolean
R1 = A - B
R0 = B - A
Return (SEL ? R1 : R0)

2. Translating into DOp code

Let’s write the associated DOp pseudocode. Keep in mind that the computation is performed homomorphically, meaning the actual values are unknown. Also remember that we only have 4-bit words available. 

To compute x - y without overflow, we restrict the result to 3 bits using a pseudo two’s complement representation. In practice, we rewrite it as: x + (‘b100 - y).

Here, bit [2] is the opposite of the sign: (0) represents a negative value, and (1) represents a positive value.

Since the comparison is not an arithmetic operation, we need a LUT to implement this function which will be applied during the PBS. To do this, we first gather the 2 values to be compared into the same 4-bit word.

Then the PBS inputs are the LUT representing the comparison, and this word.

Selection is also non-arithmetic and therefore requires a LUT applied during another PBS.Ideally, selecting between two 2-bit values would need a 5-bit LUT input (1 bit for the selector and 2×2 bits for the data). But since only 4-bit words and 4-bit LUTs are available (the padding bit cannot be used), the selection must be split into two steps:

• Step1: For each 2-bit input, perform a PBS to select between the value and 0.
• Step 2: Add the two results together.

# Input: A, B elementary ciphertexts.
# Output: R = |A-B|, which is an elementary ciphertext.
S1  = (A << 2) + B                # Put A and B in the same 4-bit word
SEL = PBS(gt, S1)                 # Compare A and B,
    # using a PBS with “greater than” LUT.
NB  = 4 - B                       # -B over 3bits
NA  = 4 - A                       # -A over 3bits
D1  = A + NB                      # A - B over 3 bits
D2  = B + NA                      # B - A over 3 bits
M1  = (SEL << 3) + D1             # Put select and D1 in the same 4-bit word
M0  = (SEL << 3) + D0             # Put select and D0 in the same 4-bit word
S1  = PBS(if_then_else_0, M1)     # SEL ? M1[1:0] : 0
S0  = PBS(if_then_0_else, M0)     # SEL ? 0 : M0[1:0]
R   = S1 + S0
return PBS(clean, R)              # Remove the noise due to the last
                                  # addition.

The translation into DOp code is straightforward:

1  LD   R1 TS[1].0              # Load element#0 of source#0 (i.e. B) in R1
2  LD   R0 TS[0].0              # Load element#0 of source#1 (i.e. A) in R0
3  MAC  R4 R0 R1 4              # S1  = (A << 2) + B
4  PBS  R4 R4 PbsGreaterThan    # SEL = PBS(gt, D1)
5  SSUB R2 R1 4                 # NB  = 4 - B
6  SSUB R3 R0 4                 # NA  = 4 - A
7  ADD  R2 R2 R0                # D1  = A + NB
8  ADD  R3 R3 R1                # D2  = B + NA
9  MAC  R2 R4 R2 8              # M1  = (SEL << 3) + D1
10 MAC  R3 R4 R3 8              # M0  = (SEL << 3) + D0
11 PBS  R2 R2 PbsIfThenElse0    # S1  = PBS(if_then_else_0, M1)
12 PBS  R3 R3 PbsIfThen0Else    # S0  = PBS(if_then_0_else, M0)
13 ADD  R2 R2 R3                # R   = S1 + S0
14 PBS  R2 PbsNone              # R   = PBS(clean, R)
15 ST   TD[0].0 R2              # Store R2 in element#0 of destination#0 

Note: This custom IOp is shown as an example. A more efficient approach would be to use a single PBS with a LUT, since |A-B| with 2-bit inputs is just a 4-bit input → 2-bit output function.

See the DOp documentation for more details. Remember that a LUT can encode any 4-bit input → 4-bit output function, and you can define your own if it’s not already in the catalogue.

3. Execution on the HPU

Now let’s look at the execution of this code by the HPU.

1. HPU initialization

The host prepares the HPU for the computation.

• Configure it.
• Load the cryptographic keys
• Load the DOp in HPU memory, in the program area.
• Associate the Dop to the custom IOp 0x01.

Note that in practice, the whole DOp catalogue is loaded. Thus the associated IOp are ready for usage.

2. Process

• The host loads A and B in HPU data memory at offsets 0x4 and 0x8.
  
• The host starts the computation, by sending the IOp to be executed to the HPU.

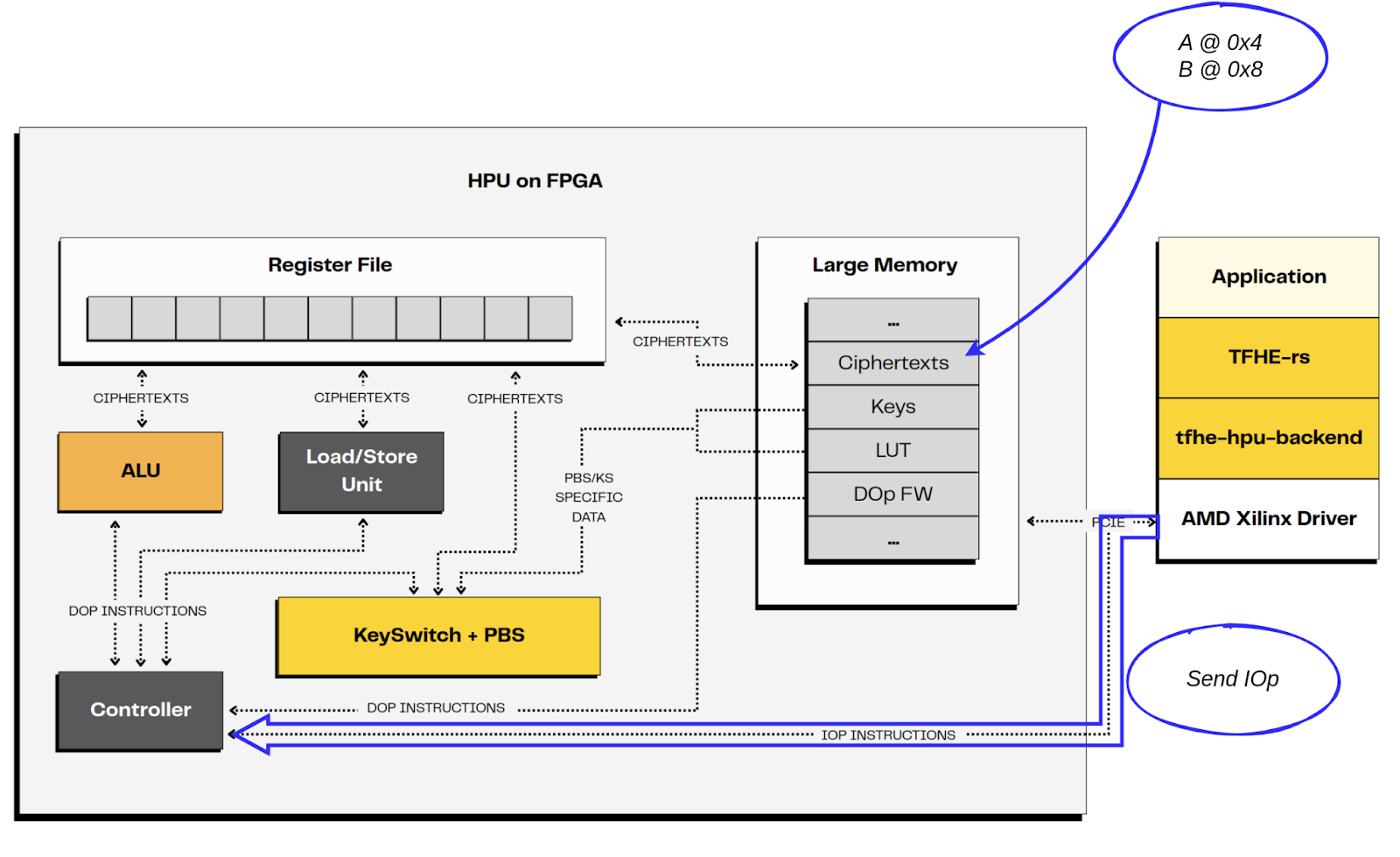
3. Execution

• The IOp is translated into the DOp code by the controller. In current implementation, this consists in retrieving the DOp code in memory from the IOp identifier.
• The controller is in charge of distributing the DOp to the corresponding Processing Element (PE). The controller has a look-ahead window. It is able to dispatch independent instructions to several PEs in parallel. This is the case for DOp#4 and #5 which are independent, and targeting different PEs.

‍

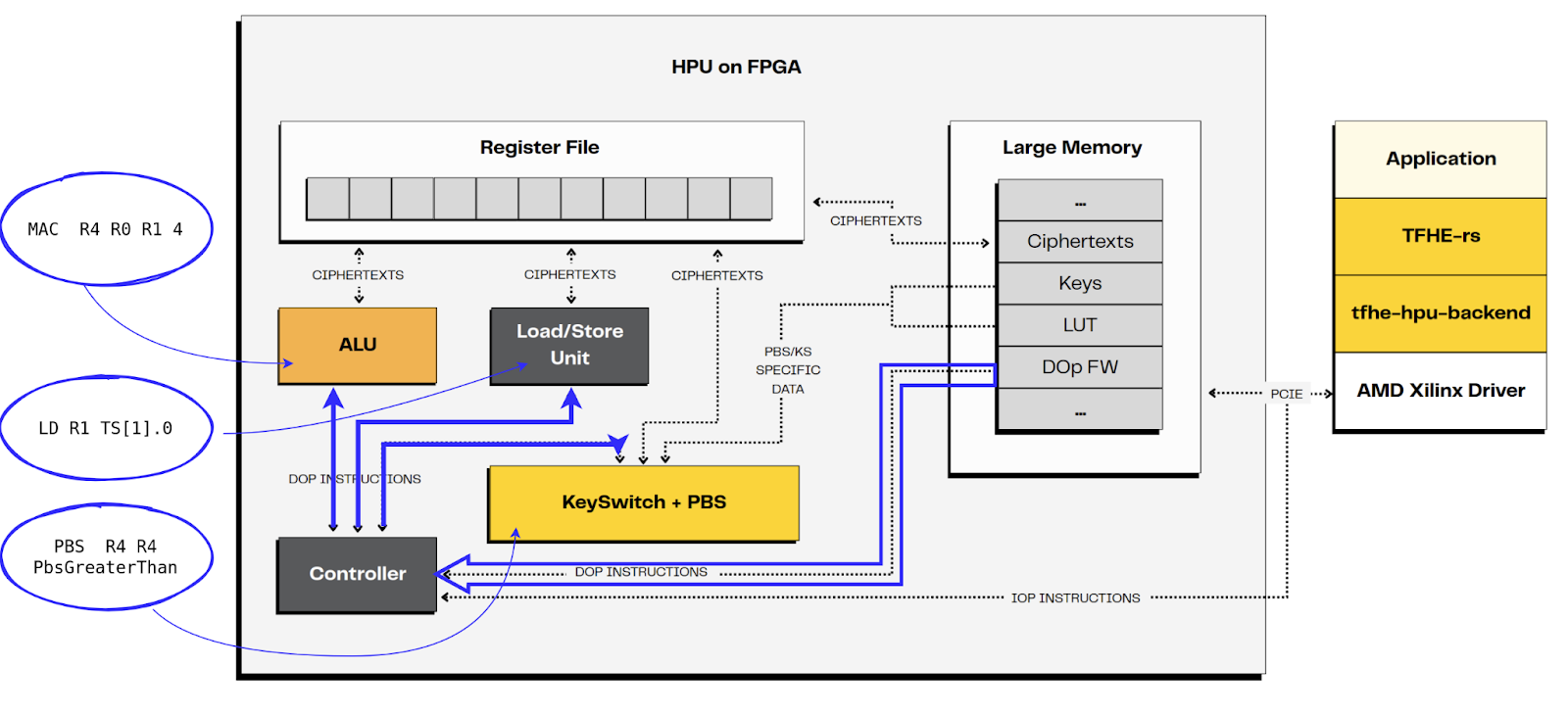
4. The controller informs the host of the end of the IOp program.

5. The host retrieves the result in HPU data memory, here in offset 0x0.

As you have noticed, the first step to use the HPU is to define the IOp code to be executed, and eventually the associated DOp code, if the operation is not already available.

Conclusion

The HPU bridges cutting-edge cryptography and hardware acceleration. By combining programmable operations (IOp/DOp), noise management (PBS/KS), and parallel execution, it enables developers to perform complex encrypted computations efficiently.

Whether you’re a researcher, a developer, or simply curious, you can start experimenting today with the available tools and tfhe-rs backend. No FPGA? Try the mockup to emulate HPU behavior.

All that’s left is to write some code!

Additional links

• Check out Zama HPU GitHub
• Read the HPU Documentation
• Follow Zama on X for latest news