Encrypted Matrix Inversion with Concrete

× During the third season of the Zama Bounty Program, we challenged our users to create an algorithm for encrypted Matrix inversion with Concrete. Github user LCressot successfully completed this bounty, and this blog post is an introduction for his contribution.

The Zama Bounty Program

1. Introduction

As stated in the original bounty subject, Matrix inversion is a mathematical operation that is vital for many use-cases: numerical optimization, solving systems of equations, learning regression models, principal-component analysis.  

The accepted submission, introduced in this blogpost, implements:

• A fixed point class to replace floating  point computations called QFloat;
• A matrix inversion algorithm based on LU-decomposition;
• An optimized algorithm for the special case of 2x2 matrices.

2. Clear Matrix Inversion background

From a theoretical point of view, computing the inverse $A^{-1}$ of a matrix $A$ consists in finding a matrix $A^{-1}$ such that $A \times A^{-1} = I$ where $I$ denotes the Identity Matrix.

For a 2x2 matrix, the formula is directly given by:

$$\begin{pmatrix}a & b \\ c & d\end{pmatrix}^{-1} = \frac{1}{ad-bc}\begin{pmatrix}d & -b \\ -c & a\end{pmatrix}$$

where $ad - bc$ is called the determinant and $\begin{pmatrix}d & -b \\ -c & a\end{pmatrix}$ the adjoint matrix.

Exemple:$$\begin{pmatrix}1 & 2 \\ 3 & 4\end{pmatrix}^{-1}= \frac{1}{-2}\begin{pmatrix}4 & -2 \\ -3 & 1\end{pmatrix}$$

2.1. Fixed Point representation

As you see in the previous example, to compute an inverse matrix, float numbers are required and currently Concrete only supports integers. The submission relies on replacing floats with fixed points with sufficient precision to represent the divisions performed by the algorithm. A new class was created for this purpose,  called QFloat.

QFloat class represents fixed point numbers as an array of integers, allowing operations like additions, multiplications, etc. The representation can utilize any chosen base (such as base 2, which is binary) and any level of precision (the longer the array and the larger the base, the more precise the QFloat representation).

The array is split between an integer part and a decimal part (after the decimal point). For instance, 34.42 = 34 + 0.42. The length of the integer part must be provided along with the total length of the array to create a QFloat. The longer the integer part, the higher the QFloat can go to encode a number. The longer the total length (meaning the longer the decimal part), the more precise it can get.

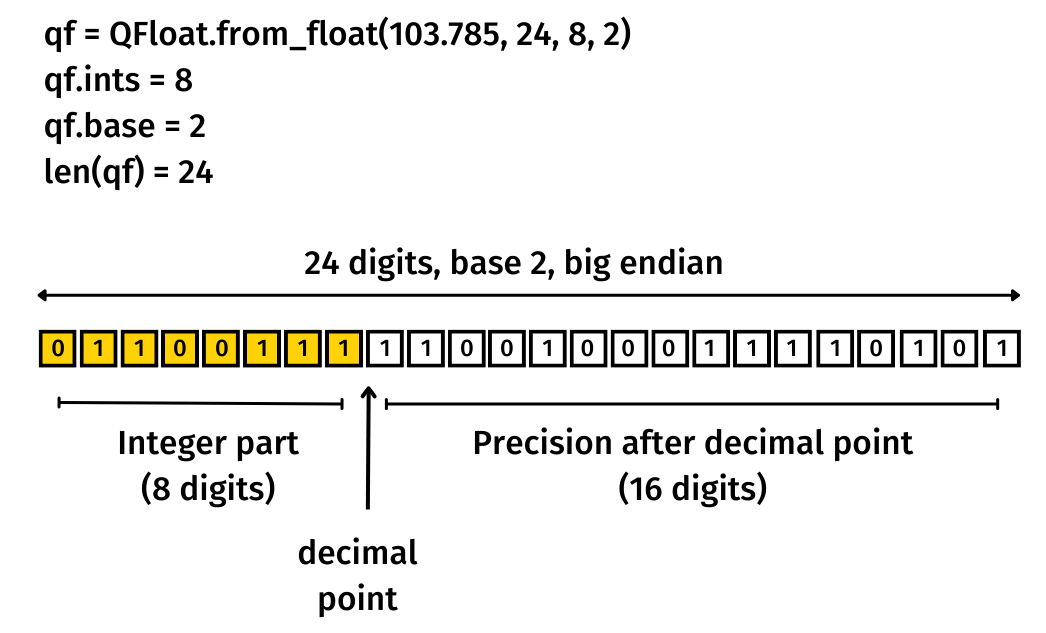
The number of digits for the integer part and for the precision after the decimal point have to be set according to the use case.

2.2. QFloat operations

Let's introduce one of the QFloat operation implementations: QFloat addition (in file  [.c-inline-code]qfloat.py[.c-inline-code], method in place addition  [.c-inline-code]__iadd__ [.c-inline-code]). For this blogpost, we will only focus on the regular case of adding a QFloat to another QFloat and let user check the code for all other variations:

    def __iadd__(self, other):
     """
     Sum with another QFLoat or single integer, in place
     """
     […]
     # multiply array by sign first (becomes 0 if sign is 0)
     self._array *= self._sign
     […]
     # default case
     else: 
        self.self_check_convert_fhe(other.encrypted)
        self.check_compatibility(other)
        self._array = self._array + other._array * other._sign

     self._is_base_tidy = False
     self._sign = None
     self.tidy()

     return self

[.c-inline-code]check_compatility[.c-inline-code] will make sure both QFloat have the same encoding (number of digits, digits for the integer part…):

   self.check_compatibility(other)

then each array values are added together (ignoring overflow for the moment):

   self._array = self._array + other._array * other._sign

[.c-inline-code]tidy[.c-inline-code] will rearrange the array so that every value is in $[0, base[$ and define the sign. First by calling [.c-inline-code]base_tidy[.c-inline-code] that will handle overflow and set every values in $]-base, base[$:

    def tidy(self):
        if not self._is_base_tidy:
            self.base_tidy()

Then, make all values the same sign. To do this, we consider that:

• A QFloat $F$ is the sum of its positive and negative parts: $F = P + N$;
• As $N$ is negative, we also have $F = P - |N|$, where both $P$ and $|N|$ are positive.

So we can use the regular subtraction algorithm in the current base: base_p (method[.c-inline-code]bpa.base_p_subtraction[.c-inline-code])

       - if $P < |N|$, we can use $F = -1 \times (|N| - P)$ so the subtraction algorithm works.

         P = self._array * (self._array >= 0)
        abs_N = -1 * (self._array * (self._array < 0))

        P_minus_abs_N, is_negative = bpa.base_p_subtraction(P, abs_N, self._base, True)
        is_positive_or_0 = 1 - is_negative
        self._array = (
            is_positive_or_0 * P_minus_abs_N
            + is_negative * bpa.base_p_subtraction(abs_N, P, self._base)
        )

        self._sign = 2 * is_positive_or_0 - 1

and return a proper QFloat.

Note that for a base 2, 16 bits integer part and 16 bits decimal part, the function costs 672 Programmable bootstrapping.  [.c-inline-code]qfloat.py[.c-inline-code] implements all arithmetic operations and comparisons for QFloat.

3. Algorithm for 2x2 matrices

Back to our matrix inversion, let’s start with a simple 2x2 matrix, this first implementation could be found in [.c-inline-code]qfloat_matrix_inversion.py[.c-inline-code] under function:

def qfloat_inverse_2x2(qfloat_M, qfloat_len, qfloat_ints):

where:

• qfloat_M is the input Matrix as an array of arrays of QFloat values;
• qfloat_len is the number of digits;
• qfloat_ints is the number of digits for the integer part.

3.1. Compute determinant

To compute the two multiplications we just call the multiplication method of QFloat, keeping room for the integer part (sum of the size of the integer part, here [.c-inline-code]2*qfloat_ints[.c-inline-code]) and then allow some room for the decimal part to keep some precision (arbitrarily set to 3 digits here).

ad = QFloat.from_mul( a, d, 2 * qfloat_ints + 3, 2 * qfloat_ints)
bc = QFloat.from_mul(b, c, 2 * qfloat_ints + 3, 2 * qfloat_ints)
det = ad + bc.neg()  # determinant of M in 17 bits

3.2. Invert determinant

The important part of this operation is to notice that we assign the full length of the result QFloat to the decimal part (as we don’t need any integer part) to have the best possible precision (inversion source code is in qfloat.py)

det_inv = det.invert(1, qfloat_len, 0)

3.3. Compute inverse matrix

Now that we have the value of the determinant’s inverse, we need to apply it to the adjoint matrix to get the resulting inverse Matrix:

mul = lambda x, y: QFloat.from_mul( x, y, qfloat_len, qfloat_ints)
 M_inv = [
     [mul(d, det_inv), mul(b, det_inv).neg()],
     [mul(c, det_inv).neg(), mul(a, det_inv)],
 ]

4. Larger Matrix Inversion with LU decomposition

Unfortunately, the simple approach for 2x2 matrices does not scale well and for larger matrices another strategy has been implemented: Inversion with Lower Upper decomposition (LU decomposition). 

A LU decomposition refers to the decomposition of $A$, with proper row and/or column orderings or permutations, into two factors – a lower triangular matrix $L$ and an upper triangular matrix $U$ (see LU_decomposition for more details). 

$$A = L \times U$$

4.1. Compute the LU decomposition 

The theory of LU decomposition is not detailed here, only the necessary parts to understand the submission code are discussed. The LU decomposition is performed in the submission  with Doolittle’s algorithm which,  in short, is a variant of LU decomposition where the diagonal of the L matrix is filled only with ones.

$L$ looks like $$L = \begin{pmatrix}1&0&0\\\ l_{10} & 1 & 0 \\ l_{20} & l_{21} & 1\end{pmatrix}$$

and $U$ like $$U = \begin{pmatrix}u_{00} & u_{01} & u_{02}\\ 0 & u_{11} & u_{12}\\\ 0 & 0 & u_{22}\end{pmatrix}$$

as $A = L \times U$  (more exactly a permutation of $A$ noted Permuted Matrix or $PM$ in the code with $P \times A = PM = L \times U$, $P$ being the Permutation Matrix).

    # Create the pivot matrix P and the multiplied matrix PM
    P = pivot_matrix(M)
    PM = P @ M

$$A = L \times U$$$$ \begin{pmatrix}a_{00} & a_{01} & a_{02}\\ a_{10} & a_{11} & a_{12}\\\ a_{20} & a_{21} & a_{22}\end{pmatrix} = \begin{pmatrix}1&0&0\\\ l_{10} & 1 & 0 \\ l_{20} & l_{21} & 1\end{pmatrix} \times \begin{pmatrix}u_{00} & u_{01} & u_{02}\\ 0 & u_{11} & u_{12}\\\ 0 & 0 & u_{22}\end{pmatrix}$$

$$ \begin{pmatrix}a_{00} & a_{01} & a_{02}\\ a_{10} & a_{11} & a_{12}\\\ a_{20} & a_{21} & a_{22}\end{pmatrix} = \begin{pmatrix}u_{00} & u_{01} & u_{02}\\\ u_{00}l_{10} & u_{01}l_{10}+u_{11} & u_{02}l_{10}+u_{12} \\\ u_{00}l_{20} & u_{01}l_{20}+u_{11}l_{21} & u_{02}l_{20}+u_{12}l_{21}+u_{22} \end{pmatrix}$$

Except for the first row that is directly deduced, we could compute U elements with the following formula: $$u_{ij} = a_{ij} - \sum_{k=0}^{i-1} u_{kj} l_{ik}$$

We could find the corresponding code inside the [.c-inline-code]qfloat_lu_decomposition function[.c-inline-code] iterating over all columns for rows up to the diagonal:

    for j in range(n):
        for i in range(j + 1):
            if i > 0:
                s1 = qfloat_list_dot_product(
                    [U[k][j] for k in range(0, i)],
                    [L[i][k] for k in range(0, i)],
                    tensorize,
                )
                U[i][j] = PM[i][j] + s1.neg()
            else:
                U[i][j] = PM[i][j].copy()

Once we have a value of a column for U we could compute the value of l for the same column, with the particular case of the first column that is a direct division. The formula for L is the following one: $$l_{ij} = \frac{1}{u_{jj}} (a_{ij} - \sum_{k=0}^{j-1} u_{kj} l_{ik})$$

Translated in this piece of code iterating over all columns, for rows starting from the diagonal to the last one:

    for j in range(n):  
        for i in range(j + 1, n):
            if j > 0:
                s2 = qfloat_list_dot_product(
                    [U[k][j] for k in range(0, j)],
                    [L[i][k] for k in range(0, j)],
                    tensorize,
                )
                L[i][j] = (PM[i][j] + s2.neg()) / U[j][j]
            else:
                 L[i][j] = PM[i][j] / U[j][j]

Now we have $L$, $U$ along with $P$ that we omit in this explanation that is the pivot matrix such that $P \times A = L \times U$ meaning $A = P^{-1} \times L \times U$, $P$ being a permutation matrix $P^{-1} = transp(P)$ explaining the last operation:

    P = np.transpose(P)

4.2. compute inverse qfloat_lu_inverse

Now that we have decomposed our Matrix $A$ in $transp(P) \times L \times U$, computing the inverse of $A$ is looking for $X$ such that:

$A \times X =  I$, $A$  being equal to $transp(P) \times L \times U$

$transp(P) \times L \times U \times X = I$

$L \times U  \times X = P$

We will start by forward substitution and finding $Y$ so that $L \times Y = P$

then backward and solving $X$ so that  $U \times X = Y$

4.2.1 Forward substitution

Forward substitution will solve $Y$ so that: $L \times Y = P$ that could be solved linearly and translated to the following piece of code:

 Y = zero_list_matrix(n)
    for i in range(n):
        # Y[i, 0] = P[i, 0] / L[0, 0]
        # dividing by diagonal values of L is useless because they are equal to 1
        Y[i][0] = P[i][0].copy()
        for j in range(1, n):
            # Y[i, j] = (P[i, j] - np.dot(L[j, :j], Y[i, :j]))
            Y[i][j] = P[i][j] - qfloat_list_dot_product(
                [L[j][k] for k in range(j)], [Y[i][k] for k in range(j)], tensorize
            )

4.2.2. Backward substitution

Now we will solve the backward substitution with $U \times X = Y$ with the following piece of code:

    for i in range(n - 1, -1, -1):
        # X[i, -1] = Y[i, -1] / U[-1, -1]
        X[i][-1] = Y[i][-1] / U[-1][-1]
        
        for j in range(n - 2, -1, -1):
            # X[i, j] = (Y[i, j] - np.dot(U[j, j+1:], X[i, j+1:])) / U[j, j]
            temp = Y[i][j] - qfloat_list_dot_product(
                [U[j][k] for k in range(j + 1, n)],
                [X[i][k] for k in range(j + 1, n)],
                tensorize,
            )
         X[i][j] = temp / U[j][j]

$X$ being our result as the inverse matrix of $A$.

5. FHE Optimization

The algorithm in FHE is exactly the same as the clear one. To improve performances two improvements were added:

• Whenever it’s possible to parallelize the computation, it will be done with a keyword [.c-inline-code]tensorize[.c-inline-code],  it will gather all multiplications of QFloat that could be done in parallel to distribute it better over the available cores (something Concrete compiler is very good at).
• When a division is required instead of doing the division each time, the inverse value of the divider is computed once before the loop and then divisions are replaced with multiplications by this precomputed inverse value. It’s a tradeoff, it goes faster but you lose precision as seen in the precision benchmarks provided:
  

The values of the precision parameters are listed below :

6. Benchmark

Here are the performance of both algorithms, given in seconds for 2x2 and 3x3 matrices:

As you could see in this table, compilation is very slow for a 3x3 matrices, it’s due to the loop unrolling pass on the initial program, which creates a huge number of nodes to process. There is still some room for improvement, notably on the tensorized version that in its current form improves the compilation process but not the execution time.

7. Next Steps

The current status of the matrix inversion is not generic enough to be integrated, as it, in concrete-python. It is still a great example of a compilation heavy use case with a lot of loops to unroll and would certainly serve in the future as a good test for improvement on the compilation front. It also introduces a good way to deal with fixed point numbers.

You could continue exploring this topic by jumping into the code and if you are interested in these FHE challenges, give it a try during next bounty season